분할정복법

주어진 문제를 분할하여 해결하는 방법을 말한다. 즉, 한 번에 해결하기 어려운 문제를 작은 단위의 부문제들(subproblems)로 쪼개어 해결하는 방법이다.

 

일반적인 재귀적 해법과 분할정복법의 차이

-문제를 한 조각과 나머지부분으로 나누는 것이 아니라, 거의 균등한 크기의 부분 문제로 나눈다는 점이다.

 

 

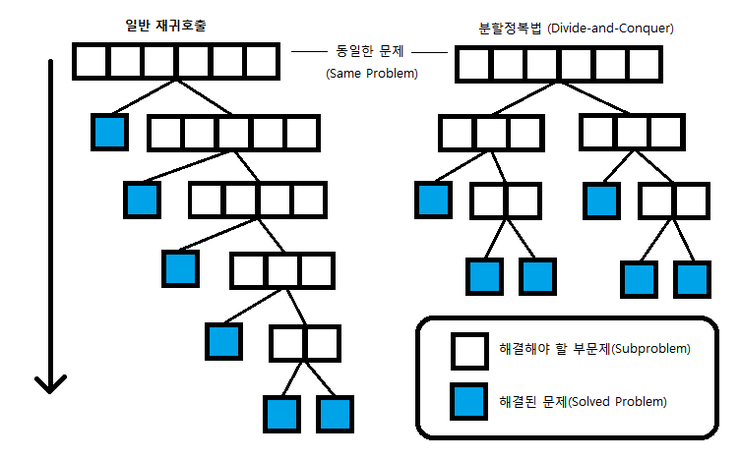
★분할정복 알고리즘에는 보통 다음과 같은 세 가지 과정이 있다.

①     문제를 더 작은 문제(부문제)로 분할 (Divide)

②     각 부문제에서 구한 답을 분할하기 전의 원래 문제에 대한 답이 되도록 합병하는 과정 (Merge)

③     더 이상 쪼갤 필요가 없거나 쪼갤 수 없는 문제에 대해 답을 구하는 과정 (Base case)

 

★ 분할정복법을 적용할 필요성이 있는지 알아보려면 다음의 두 가지 조건을 검사해보면 된다.

①     문제를 여러 부문제들로 쪼개는 것이 가능한가? (Divide)

②     부문제들의 답을 조합하여 본래 문제의 답을 효율적으로 구할 수 있는가? (Merge & Conquer)

 

위 조건 중 2번에서 '효율적'이라는 말을 강조한 이유는 분할정복법을 적용시킬 수 있다고 한들 무식하게 푸는 방법보다 비효율적이면 이 방법을 사용하는 의미가 없기 때문이다. 그 말은 즉, 분할정복법의 장점은 처리 속도라는 것이다. 간단한 예제를 통해서 정말로 처리 속도에 이득이 있는지를 확인해보자. 분할정복법은 퀵 정렬(Quick Sorting), 합병정렬(Merge Sorting), 이진검색(Binary Search), 고속퓨리에변환(FFT), 유클리드 호제법(Euclidean algorithm) 등이 있다.

 

출처 : http://kugistory.net/76

 

 

[출처] 분할정복법|작성자 튜기